There are several ways to find square root of a given number. The most useful and practical method for the students to use during the examination is ‘prime factorization’ method. This is because in NAT examinations students are generally given ‘perfect squares’ even in simple terms as well as in fractions including mixed numbers.

Prime Factorization Method

Step-by-Step:

Example 1:

Step 1: Prime factorization

144 = 2 × 2 × 2 × 2 × 3 × 3

Or grouped:

144 = (2×2) × (2×2) × (3×3)

Step 2: Take one number from each pair:

Example 2:

Factorization:

900 = 2 × 2 × 3 × 3 × 5 × 5

Making pairs

(2 × 2), (3 × 3), (5 × 5)

Take one from each:

If the number is not a perfect square, factorization won't give a whole number. But it can still help to simplify square roots.

Findings square roots of fractions and mixed numbers

Let's explore how to use the factorization method to find or simplify the square roots of fractions and mixed numbers.

This method works similarly to whole numbers, but we handle numerators and denominators (or whole and fractional parts) separately.

Factorization Method for Fractions

Given a fraction:

Use prime factorization for both a and b separately, then take the square root. See given example below.

Example 1: Find

49 = 7 × 7 → √49 = 7

64 = 2 × 2 × 2 × 2 × 2 × 2 → √64 = 8

So:

​

Final Answer: 7/8

If It’s Not a Perfect Square:

You can simplify the square root, but you may not get an exact number.

Example 2: Simplify

Step 1: Simplify the fraction first

Step 2: Factor and find roots

9 = 3 × 3 → √9 = 3

25 = 5 × 5 → √25 = 5

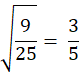
Final Answer: 3/5

Factorization Method for Mixed Numbers

Step-by-Step:

Convert the mixed number to an improper fraction.

Use prime factorization on the numerator and denominator.

Apply square root to each and simplify.

Example 3: Find

Step 1: Convert to improper fraction:

​

Step 2: Factorize:

9 = 3 × 3 → √9 = 3

4 = 2 × 2 → √4 = 2

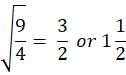
Final Answer: 3/2 or 1½

Example 4: Find

Step 1: Convert to improper fraction:

17 is prime, 9 = 3 × 3

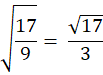Final Answer: ​​ (can’t simplify further)